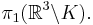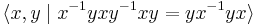Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,
Other conventions consider knots to be embedded in the 3-sphere, in which case the knot group is the fundamental group of its complement in S'3
Contents |
Properties
Two equivalent knots have isomorphic knot groups, so the knot group is a knot invariant and can be used to distinguish between inequivalent knots. This is because an equivalence between two knots is a self homeomorphism of  isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).
isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).
The abelianization of a knot group is always isomorphic to the infinite cyclic group Z; this follows because the abelianization agrees with the first homology group, which can be easily computed.
The knot group (or fundamental group of an oriented link in general) can be computed in the Wirtinger presentation by a relatively simple algorithm.
Examples
- The unknot has knot group isomorphic to Z.
- The trefoil knot has knot group isomorphic to the braid group B3. This group has the presentation
-
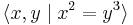 or
or 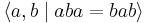 .
.
- A (p,q)-torus knot has knot group with presentation
-
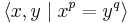 .
.
- The figure eight knot has knot group with presentation
- The square knot and the granny knot have isomorphic knot groups, yet these two knots are inequivalent.
See also
References
- Hazewinkel, Michiel, ed. (2001), "Knot and link groups", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=k055580